합성곱 신경망 (Convolution Neural Network) - CNN의 동작 방식

본 포스팅은 Ian Goodfellow 등 2인이 저술한 심층학습(Deep Learning Adaptive Computation and Machine Learning)및 오일석 저술의 기계학습 등을 기반으로 작성합니다.

 

지난 포스팅에서는 합성곱 신경망의 합성곱에 대해서 알아봤습니다. 이번 포스팅에서는

 

1. 합성곱이 무엇인가?

2. 합성곱을 사용하는 이유는 무엇인가?

3. 그래서 CNN은 어떻게 동작하는가?

 

이번에는 CNN의 동작 방식에 대해서 이해해보도록 하죠.

CNN의 동작 방식을 잘 설명한 예시입니다. 차차 이야기를 풀어보도록 하죠.

 

다음 그림은 Mnist Dataset에서 추출한 손글씨 그림입니다. 데이터 사이언스를 공부하는 이들에게는 아주 익숙한 데이터입니다. 이 그림은 손글씨의 숫자를 구별해내는 알고리즘을 개발하는데 큰 도움을 주었죠. 이 그림은 28*28 사이즈의 픽셀로 구성되어 있고, 이는 28*28 사이즈의 행렬로 나타낼 수 있습니다. 즉 2차원 이미지 -> 행렬로 나타내는 것이죠. 

 

다음과 같은 이미지와 필터가 있다고 가정합시다. 이미지의 크기는 5*5, 그리고 CNN에는 필터가 있다고 했죠? 그 필터의 크기를 3*3으로 가정합시다. 우리는 오른쪽의 필터를 이용해 왼쪽의 이미지를 모두 훑어줄 것입니다. 입력값 이미지의 모든 영역에, 필터와 내적 계산을 진행한다고 하는 거죠. 

가장 먼저 왼쪽 위 영역부터 필터와 이미지의 내적 계산을 수행합니다. 결과값은 4이고 이를 분홍색 행렬의 왼쪽 위 영역에 넣습니다. 

그리고 필터를 왼 편으로 한 칸 옮겨서 같은 내적 계산을 수행합니다. 이를 전체 이미지에 적용한 것이 분홍색 행렬의 결과값입니다. 그런데 결과값을 잘 보면... 5*5 사이즈의 이미지 행렬이 3*3 사이즈로 줄어들었죠? 이는 가로 5사이즈인 블록에 3사이즈 블록이 3번밖에 못 들어가는 것과 같습니다. 어떻게 보면 당연하죠. 수식으로 나타내볼까요?

입력값: d_1 x d_2
필터: k_1 x k_2
결과값: (d_1 - k_1 + 1) x (d_2 - k_2 + 1)

그러면 이미지의 크기가 줄어들면 무슨 문제가 있을까요? 이미지가 손실되는 부분이 발생한다는 것입니다. 이런 문제점을 해결하기 위해서 5*5 행렬의 외곽에 원소 0을 집어넣은 7*7 행렬을 만들어서 이를 보완합니다. 이를 Zero Padding이라고 합니다. 

다음과 같이 말이죠. 이러면 결과값이 (d_1 - k_1 + 2) x (d_2 - k_2 + 2) = (7 - 3 + 1) * (7 - 3 + 1) = 5*5  행렬이 되겠네요.

 

위에 계산에서는 필터를 한 칸씩 옮겼죠? 사실 필터를 여러 칸 옮기는 것도 가능합니다. 이를 Stride라고 합니다. Stride-1이 Default이고 Stride값이 커지면 커질 수록 건너뛰는 칸이 커지므로 이미지의 크기는 작아집니다.

 

이 CNN은  R,G,B 컬러를 모두 포함한 3차원 이미지 텐서에도 사용이 가능합니다. 다만 주의할 점은 입력의 채널 수와 필터의 채널 수가 같아야한다는 것입니다. 연산은 동일하게 내적을 사용하고, 결과값은 (d_1 - 2) x (d_2 - 2) 사이즈의 행렬로 계산이 됩니다. 

 

CNN의 구조입니다.  이미지를 입력한 후 컨볼루션층과 활성함수를 지나 Pooling 층을 지납니다. 그리고 Flatten 과정을 거치고 Fully-Connected된 레이어에서 분류를 진행한 후 최종적으로 활성함수를 지나 결과값을 냅니다. 

 

1st Convolution Layer + Activation Function

가장 먼저 컨볼루션 층과 활성함수입니다. 28*28 사이즈의 mnist 데이터에, 10개의 5*5 사이즈의 필터를 씌워서 24*24 사이즈의 결과값 10개를 얻어냈습니다. 그리고 이 결과값에 활성함수로 ReLU 등의 함수를 적용합니다.

1st Pooling Layer

그리고 Pooling Layer를 지납니다. 이 전 단계에서 10개의 필터를 지나면서 10개의 이미지 결과값을 만들어냈습니다. 그런데 문제는 값이 너무 많다는 것입니다. 이로 인해서 고안해낸 것이 Pooling입니다. 각 결과값의 차원을 축소하는 것이죠. 차원 축소의 핵심은 특징을 잘 살리면서 데이터를 압축해야한다는 것입니다. Pooling의 방법은 크게 두 가지가 있는데, Max Pooling과 Average Pooling이 있습니다. Pool 사이즈를 결정한 후 (이 그림에서는 2 x 2로 결정했네요.) 그 Pool 안에서 가장 큰 값(Max), 그 Pool의 평균값(Average)를 가져와 결과값의 크기를 줄입니다. 

Max Pooling VS Average Pooling

2nd Convolution Layer

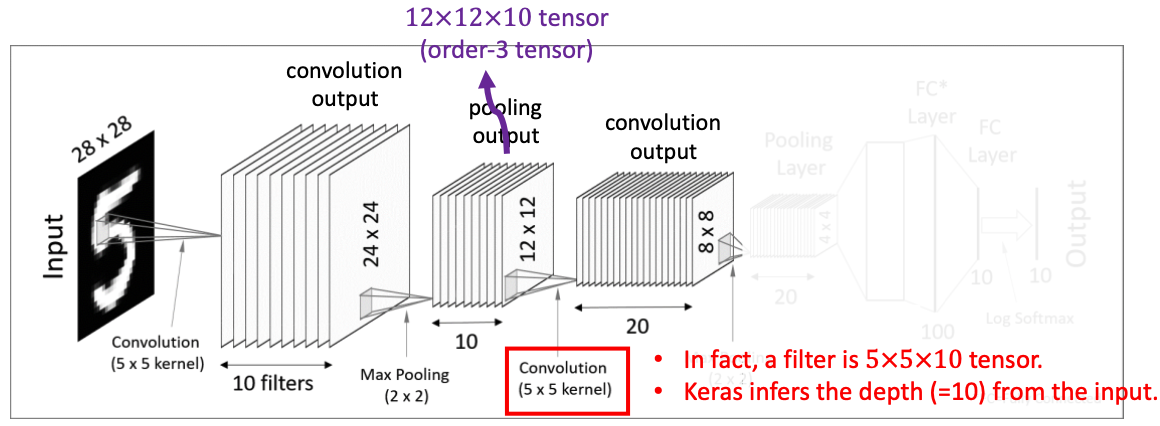
두 번째 컨볼루션 층부터는 텐서 계산입니다. 이전 Pooling Layer에서 얻어낸 12 * 12 * 10 텐서를 대상으로 5 * 5 * 10 사이즈의 텐서 필터를 20개 사용합니다. 결론적으로 8 * 8 사이즈의 결과값 20개를 얻어냅니다. 

2nd Pooling Layer

두 번째 Pooling Layer입니다. 4 * 4 사이즈의 결과값 20개를 얻어냅니다. 

그리고 4*4*20의 텐서를 일자 형태로 쭉 펼쳐줍니다. 이를 Flatten이라고 합니다. 각 세로줄을 일렬로 쭉 세워주는 겁니다. 그러면 320 차원의 벡터 형태가 되겠군요. 이렇게 1차원 형태로 변환해도 되는 이유는 4*4 크기의 이미지가 이미지 자체가 아닌 이미지에서 얻어온 특이점 데이터가 되므로, 변형을 해도 큰 문제가 없다고 합니다. 

 

그리고 마지막으로 하나 이상의 Fully-Connected Layer를 적용시키고, 활성화함수로 Softmax Function을 통과시키면 최종 결과물을 출력하게 됩니다!

 



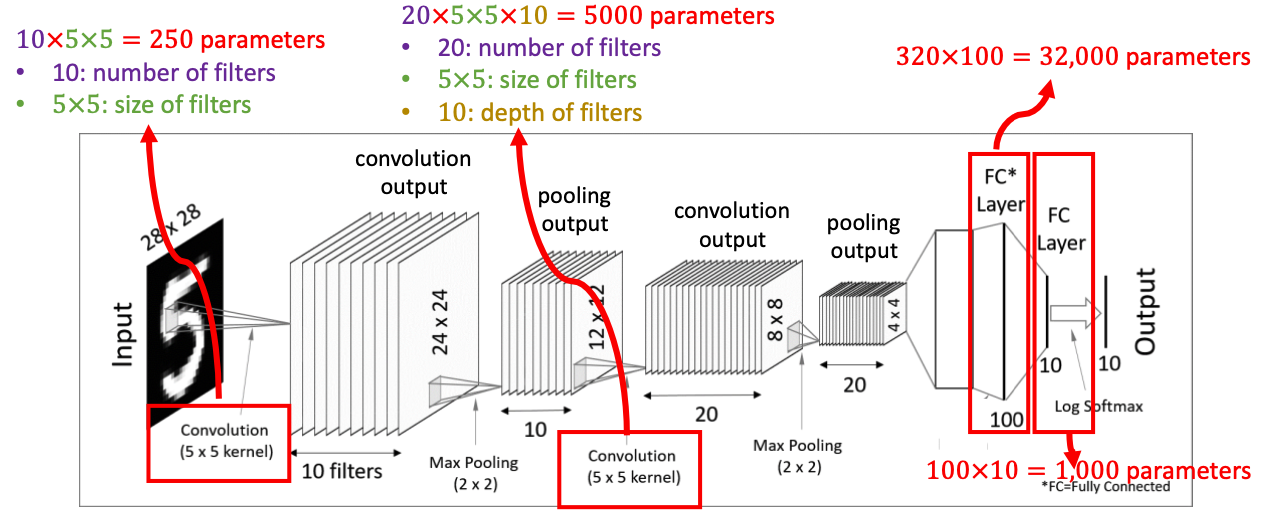
학습 가능한 매개변수들이 총 몇 개가 되는지 체크해볼까요?

1. 첫 Convolution 과정에서 5*5 필터 10개를 사용했음 = 250개

2. Pooling Layer는 단순히 차원축소이므로 매개변수 없음

3. 두번째 Convolution 과정에서 5*5*10 크기의 텐서 필터 20개 사용 = 5000개

4. Flatten 과정에서 32000개, 1000개가 추가

 

결국 학습 가능한 매개변수의 경우의 수는 38,250개가 넘겠네요.